Aljabar Boolean dan Karnaugh Map

Kuliah Organisasi Sistem Komputer
JUDUL ARTIKEL : ALJABAR BOOLEAN DAN KARNAUGH MAP

Tulisan ini ditujukan untuk : menyelesaikan tugas individu pada http://uzi-online.blogspot.com/2000/11/kuliah-organisasi-sistem-komputer.html

ALJABAR BOOLEAN

Aljabar boolean merupakan aljabar yang berhubungan dengan variabel-variabel biner dan operasi-operasi logik. Variabel-variabel diperlihatkan dengan huruf-huruf alfabet, dan tiga operasi dasar dengan AND, OR dan NOT (komplemen). Fungsi boolean terdiri dari variabel-variabel biner yang menunjukkan fungsi, suatu tanda sama dengan, dan suatu ekspresi aljabar yang dibentuk dengan menggunakan variabel-variabel biner, konstanta-konstanta 0 dan 1, simbol-simbol operasi logik, dan tanda kurung.

          Suatu fungsi boolean bisa dinyatakan dalam tabel kebenaran. Suatu tabel kebenaran untuk fungsi boolean merupakan daftar semua kombinasi angka-angka biner 0 dan 1 yang diberikan ke variabel-variabel biner dan daftar yang memperlihatkan nilai fungsi untuk masing-masing kombinasi biner.

          Aljabar boolean mempunyai 2 fungsi berbeda yang saling berhubungan. Dalam arti luas, aljabar boolean berarti suatu jenis simbol-simbol yang ditemukan oleh George Boole untuk memanipulasi nilai-nilai kebenaran logika secara aljabar. Dalam hal ini aljabar boolean cocok untuk diaplikasikan dalam komputer. Disisi lain, aljabar boolean juga merupakan suatu struktur aljabar yang operasi-operasinya memenuhi aturan tertentu.

DASAR OPERASI LOGIKA

LOGIKA :

Memberikan batasan yang pasti dari suatu keadaan, sehingga suatu keadaan tidak dapat berada dalam dua ketentuan sekaligus.

Dalam logika dikenal aturan sbb :

¨      Suatu keadaan tidak dapat dalam keduanya benar dan salah sekaligus

¨      Masing-masing adalah benar / salah.

¨      Suatu keadaan disebut benar bila tidak salah.

Dalam ajabar boolean keadaan ini ditunjukkan dengan dua konstanta : LOGIKA ‘1’ dan ‘0’

Operasi-operasi dasar logika dan gerbang logika :

Pengertian GERBANG (GATE) :

¨      Rangkaian satu atau lebih sinyal masukan tetapi hanya menghasilkan satu sinyal keluaran.

¨      Rangkaian digital (dua keadaan), karena sinyal masukan atau keluaran hanya berupa tegangan tinggi atau low ( 1 atau 0 ).

¨      Setiap keluarannya tergantung sepenuhnya pada sinyal yang diberikan pada masukan-masukannya. 

Operasi logika NOT ( Invers )

          Operasi merubah logika 1 ke 0 dan sebaliknya à x = x’

Operasi logika AND

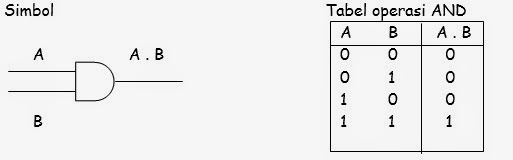
¨      Operasi antara dua variabel (A,B)

Operasi ini akan menghasilkan logika 1, jika kedua variabel tersebut berlogika 1

Operasi logika OR

Operasi antara 2 variabel (A,B)

Operasi ini akan menghasilkan logika 0, jika kedua variabel tersebut berlogika 0.

Operasi logika NOR

Operasi ini merupakan operasi OR dan NOT, keluarannya merupakan keluaran operasi OR yang di inverter.

Operasi logika NAND

Operasi logika ini merupakan gabungan operasi AND dan NOT, Keluarannya merupakan keluaran gerbang AND yang di inverter.

Operasi logika EXOR

akan menghasilkan keluaran ‘1’ jika jumlah masukan yang bernilai ‘1’ berjumlah ganjil.

Operasi logika EXNOR

Operasi ini akan menghasilkan keluaran ‘1’ jika jumlah masukan yang bernilai ‘1’ berjumlah genap atau tidak ada sama sekali.

DALIL BOOLEAN ;

1.     X=0 ATAU X=1

2.    0 . 0 = 0

3.    1 + 1 = 1

4.    0 + 0 = 0

5.    1 . 1 =  1

6.    1 . 0 = 0 . 1 = 0

7.    1 + 0 = 0 + 1 = 0

KARNAUGH MAP

Karnaugh map (disingkat K-Map) adalah suatu metode untuk menjelaskan beberapa hal tentang penghitung aljabar boolean, metode ini telah ditemukan oleh Maurice Karnaugh pada tahun 1953. Karnaugh map ini sering digunakan untuk perhitungan yang menghitung sistem pola pikir manusia dengan hal-hal yang menguntungkan (sistem pemetaan peluang).

Seperti gambar dibawah ini adalah sistem pemetaan pada bilang aljabar boolean :

gambar 1 sistem pemetaan pada karnaugh map 

pada gambar pemetaan diatas, variabel dari aljabar boolean ditransfer berdasarkan variabelnya masing-masing, dimana terjadi sistem perubahan pada beberapa kotak sehingga menghasilkan sebuah rumus 2n dengan n adalah banyaknya kotak (1,2,3,4,...). 

Dibawah sini ada beberapa sistem penghitungan aljabar boolean dengan menggunakan karnaugh map diantaranya : 

gambar 2 ∑(0); K = 0 

gambar 3 ∑(1,2,3,4); K = 1 

gambar 4 ∑(1,4); K = A′B′ + AB 

gambar 5 ∑(1); K = A′B′ 

gambar 6 ∑(2,3,4); K = A + B 

dari sistem penghitungan diatas dapat kita simpulkan bahwa sistem berdasarkan f(n) dengan n adalah nilai kolom pada tabel boolean dan pada gambar 1 menjelaskan bahwa seluruh jumlah adalah nol karena tidak ada nilai yang dapat dihitung, namun pada gambar 2 seluruh kolom terdapat nilai sehingga jumlah dari tabel tersebut adalah satu, namun jika pada gambar 3,4,5 dan 6 adalah penjumlahan pada bidang yang masing-masing memiliki nilai pada satu kolomnya, baik itu pada kolom A maupun kolom B.

REFERENSI  :
Catatan Pribadi
Materi Mata Kuliah Organisasi Sistem Komputer Bab 4 (Presentasi Kelompok 4).
Sumber Tambahan